The Problem
Last year, I worked on an interesting data synchronization problem.
- Synchronize large, somewhat significant amounts of data from a single source of truth.
- Machines are primarily online but can be offline for up to a few weeks.
- New machines are added sometimes, and they need an entire data set.
- Data comes in regular intervals. Days can vary, but weeks usually have consistent data flow.
- Although data always comes from a centralized repository, it should be able to synchronize between clients. Clients do not have new data; it's just a copy from a single source of truth.
- Clients are trustworthy; No need to validate the truthfulness or the origin of the data on the clients. (The Byzantine Generals Problem)
- Each data row has a unique state ID. Since the state ID format is Guid, there is no need to validate that each row with the same ID in different data storages is the same.
- In most cases, only the data from the last few days will be missing. Rarely, it could be old data.
The goal was to make the synchronization process between the central repository and clients and the clients themselves as simple as possible.
The Brute Force Attack
The simple solution was to send everything to everybody. The solution could not work; there was just too much data.
If I cannot send everything to everybody, I could send a list of State IDs. This approach works fine. Each client could know what is missing, and it would get only the missing data. The problem with this approach is that you are still exchanging a lot of data; there are a lot of IDs.
Buckets: The Optimized Approach
The second (and final) algorithm was to split the IDs into buckets, per (for example) a month and hash the lists of IDs. With this approach, the result would be the list of 12 hashes per year or for MD5 128 bits * 12 months. Even for 20 years of data, it would still be just 30.72kb, and the system will break long before that for various other reasons.
The main advantage of the "Buckets algorithm" is that it sends only a single, although somewhat larger, package. However, a single package from a server is enough for every client to know what is missing. The algorithm is not precise because you still need to synchronize the entire month (in our case), even if only a single data point is missing.
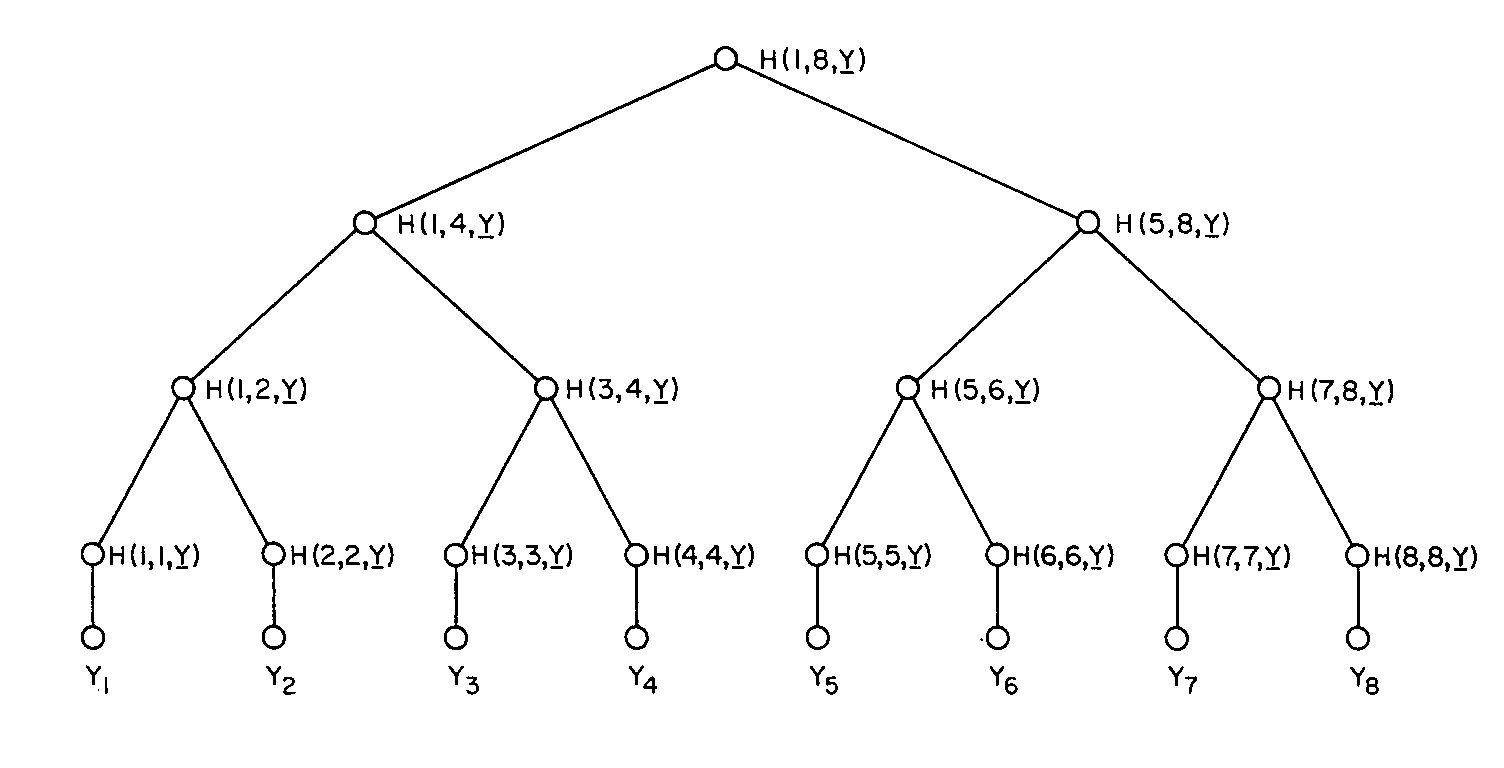
The Merkle Trees
The Merkle Trees are similar algorithms to the buckets, but we work on a hash tree instead of a list of hashes. The root note is the hash of the hashes of the second level, and second-level values are the hashes of the third, etc. It goes down to "the list of buckets" and even the hashes of the individual items.
The advantage is that for the first message, you will send 128 bits of data; if everything is up to date, that will be it. But if something is missing, we must send a list of hashes per level. Depending on the design of the tree, it could be a lot of messages. The messages would be smaller than in the bucket algorithm, but it would be at least n of them, where n is the tree's height, and in the worst-case scenario, m, where m is the total number of hashes.
In my use case, the problem with this approach is that we do not store the calculations of the hashes; they are always calculated during the call. It would be very computer intensive to recalculate all the hashes whenever you send a message, which can be one or n (height of tree).
The Merkle Trees is a more precise synchronization algorithm than "Buckets." It can pinpoint missing data to a single data point. However, it is much more chatty. Also, you need two-way communication because if the client only has a different Root Hash, it knows that something is off, but not more, so it has to request the second level of hashes, then the 3rd one, etc.
The Merkle tree is named after Ralph Merkle, who patented (US4309569A - Method of providing digital signatures) in 1979.
Although not commonly used in everyday development, Merkle Trees are used in Git, BitTorrent (Peer-to-Peer networks), and blockchain.
Ralph Merkle
Ralph Merkle is pivotal in cryptography, the best-known public-key cryptography, cryptographic hashing, and Merkle trees. Without him, the world would be a very different place. Just imagine that we got public-key cryptography just a few years later! Maybe his newer interest and research in cryonics will be as influential.
Conclusions
| Approach | Pros | Cons |
|---|---|---|
| Buckets | - Simple to implement | - Might over-fetch data |
| - Fewer round-trips | - Coarse granularity | |
| Merkle Trees | - Fine-grained sync | - Requires multiple round-trips |
| - Minimal data transfer overall |
Knowing many data structures and algorithms is advantageous for every developer. Understanding the advantages and disadvantages of the original algorithm and knowing when to modify one is even more helpful. Frequently, less perfect but easier-to-implement solutions are better.